Ceprede ha publicado su último informe mensual de predicción económica, en el que analiza las diferentes áreas, entre las que se encuentra la evolución a corto plazo del empleo.

En términos de contabilidad nacional se prevé un incremento anual en torno al 2,2% en creación de empleo en 2018, que equivaldría a aproximadamente 400.000 puestos de trabajo.

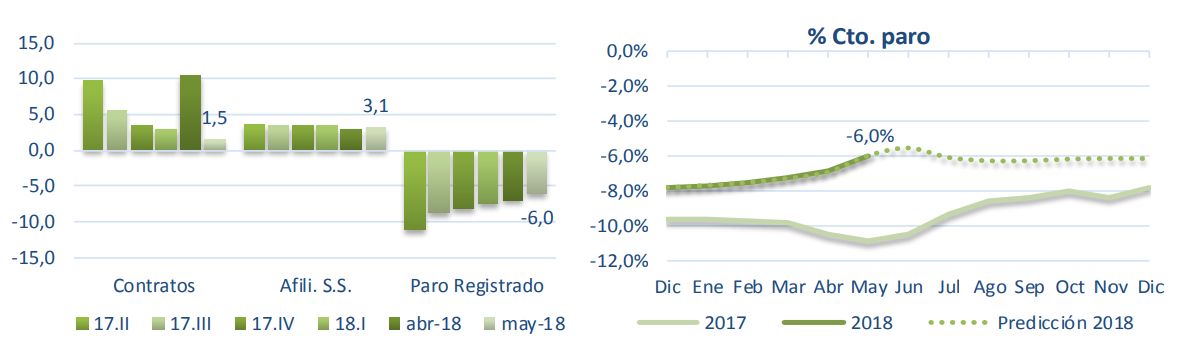
En cuanto al paro registrado, la organización estima que esa cifra se reduzca un 6% interanual en el mes de en junio, equivalente a 210.000 parados menos respecto al mismo mes de 2017, y un 6,6% en julio, con lo que se registrarían aproximadamente 230.000 parados menos.

En el conjunto de 2018 se prevé también un descenso del 6,6% del número de parados, con lo que la cifra total de desempleados se reduciría en aproximadamente 225.000 personas.

Por lo que respecta a la tasa de paro, Ceprede estima que 2018 finalice con un 15,7%, incrementándose el número de ocupados en un 2,1% respecto a 2017. Sin embargo, se prevé que en el tercer trimestre del año la tasa de paro alcance el 15%, mientras que en el segundo esta cifra se situará en el 15,7%. Por lo que respecta a 2019, se estima que el año cierre con una tasa del 14,6%.

También apunta un aumento interanual del número de contratos, que en junio supondrá un incremento del 7%, mientras que en julio será del 12,5%. En el conjunto de 2018 este aumento será del 7,6%.

Además, el informe recoge un crecimiento interanual en cuanto al número de afiliados a la Seguridad Social del 3,2% en el conjunto de 2018. Para el mes de junio, el Centro de Predicción Económica estima que este aumento también sea del 3,2%.